| ¡Vikidia te necesita! Actualmente tenemos 6582 artículos. ¡Anímate! |
Matemáticas

Las matemáticas son una área del conocimiento que estudian las propiedades y relaciones de objetos abstractos definidos mediante reglas precisas como axiomas y reglas de inferencia.
Es una disciplina que se basa en la deducción, y busca comprender las estructuras y patrones que subyacen en el mundo que nos rodea.
Las matemáticas involucran la creación y manipulación de conceptos abstractos, la formulación de teoremas y la resolución de problemas utilizando reglas lógicas y razonamiento preciso.
Las matemáticas tienen aplicaciones en una amplia gama de campos, desde la física y la ingeniería hasta la biología y la economía, y desempeñan un papel esencial en la comprensión y modelado de fenómenos naturales y artificiales.
Definición[editar · editar código]
Establecer una definición de las matemáticas y precisas claras es el fundamento de la matemática, pero definirla ha sido difícil, se muestran algunas definiciones de pensadores famosos:
René Descartes: (Cirilo Flórez Miguel, ed. Obra completa. 2004) «La matemática es la ciencia del orden y la medida, de bellas cadenas de razonamientos, todos sencillos y fáciles».
David Hilbert: (Putnam, Hilary, On the infinite. Philosophy of Mathematics, 1998). «La matemática es el sistema de las fórmulas demostrables».
Benjamin Peirce: (Nahin, Paul, The Story of , 1998). «La matemática es la ciencia que extrae conclusiones necesarias».
Bertrand Russell: (Principia Mathematica, 1913). «Las matemáticas poseen no solo la verdad, sino cierta belleza suprema. Una belleza fría y austera, como la de una escultura».
Ibo Bonilla: (¿Qué es matemática?, 2014). «La matemática es la ciencia de estructurar una realidad estudiada, es el conjunto de sus elementos, proporciones, relaciones y patrones de evolución en condiciones ideales para un ámbito delimitado».
John David Barrow: (Imposibilidad, 1999). «En el fondo, matemática es el nombre que le damos a la colección de todas las pautas e interrelaciones posibles. Algunas de estas pautas son entre formas, otras en secuencias de números, en tanto que otras son relaciones más abstractas entre estructuras. La esencia de la matemática está en la relación entre cantidades y cualidades».
Nicolás Atanes: (2018). «Los números son el lenguaje de las matemáticas».
María Moliner: (Diccionario de uso del español, 1966) «Ciencia que trata de las relaciones entre las cantidades y magnitudes y de las operaciones que permiten hallar alguna que se busca, conociendo otras.
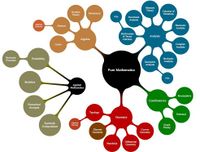
Áreas de las matemáticas[editar · editar código]
La Sociedad Estadounidense de Matemáticas distingue unas 5 000 ramas distintas de matemática. En una subdivisión escolarizada de la matemática se distinguen cinco áreas de estudio básicas: la cantidad, la estructura, el espacio, el cambio y la variabilidad que se corresponden con la aritmética, el álgebra, la geometría, el cálculo, la probabilidad y estadística.
Como señalaba Richard Courant, «es posible seguir una ruta directa a partir de los elementos fundamentales hasta puntos avanzados» para que puedan divisarse las directrices de la matemática como ciencia. Además, hay ramas de las matemáticas conectadas a otros campos, por ejemplo la lógica, teoría de conjuntos y las matemáticas aplicadas entre muchas otras tal como indica la Sociedad Estadounidense de Matemáticas.
Algunas áreas de las matemáticas son:
- Matemática recreativa: La matemática recreativa se concentra en la obtención de resultados acerca de actividades lúdicas, y también la que se dedica a difundir o divulgar de manera entretenida y motivadora los conocimientos, temas o problemas de las matemáticas.
- Historia de las matemáticas: La historia de las matemáticas es el área de estudio de investigaciones sobre los orígenes de descubrimientos en las matemáticas, de los métodos de la evolución de sus conceptos y también en cierto grado de los matemáticos involucrados.
- Teoría de conjuntos: La teoría de conjuntos estudia las propiedades y relaciones de los conjuntos: colecciones abstractas de objetos, consideradas como objetos en sí mismas.
- Educación matemática: La educación matemática es un término que se refiere tanto al aprendizaje, como a la práctica de enseñanza y evaluación de las matemáticas, así como a un campo de la investigación académica sobre esta práctica.
- Teoría de números: La teoría de números estudia las propiedades de los números, en particular los enteros, pero más en general, estudia las propiedades de los anillos de números.
- Álgebra: El álgebra estudia la combinación de elementos de estructuras abstractas acorde a ciertas reglas.
- Análisis: El análisis matemático estudia los conjuntos numéricos tanto del punto de vista algebraico como topológico, así como las funciones entre esos conjuntos y construcciones derivadas.
- Geometría: La geometría se ocupa del estudio de las propiedades de las figuras en el plano o el espacio, incluyendo: puntos, rectas, planos, politopos.
- Topología: La topología se dedica al estudio de aquellas propiedades de los cuerpos geométricos que permanecen inalteradas por transformaciones continuas.
- Combinatoria: La combinatoria pertenece a las matemáticas discretas que estudia la enumeración, construcción y existencia de propiedades de configuraciones que satisfacen ciertas condiciones establecidas. Por ejemplo la noción de grafo.
- Probabilidad: La teoría de la probabilidad estudia los fenómenos aleatorios y estocásticos.
- Estadística: La estadística es la disciplina que estudia la variabilidad, recolección, organización, análisis, interpretación y presentación de los datos, así como el proceso aleatorio que los genera siguiendo las leyes de la probabilidad.
- Análisis numérico: El análisis numérico se encarga de diseñar algoritmos para simular aproximaciones de solución a problemas en análisis matemático.
Utilidad[editar · editar código]
Las ciencias naturales han hecho un uso extensivo de la matemática para explicar diversos fenómenos observables, tal como lo expresó Eugene Paul Wigner, Premio Nobel de Física en 1963:
« El milagro de la adecuación del lenguaje de las matemáticas para la formulación de las leyes de la física es un don maravilloso que no comprendemos ni merecemos. »[1]
Galileo Galilei, en la misma línea, lo había expresado así:
« La filosofía está escrita en este enorme libro, que está continuamente abierto ante nuestros ojos (digo en el nuevo idioma), pero uno no puede entenderlo primero, uno no aprende a entender el idioma y a conocer los caracteres en que está escrito. Está escrito en lenguaje matemático, y los caracteres son triángulos, círculos y otras figuras geométricas, sin las cuales es imposible entender una palabra. »
Mediante la abstracción y el uso de la lógica en el razonamiento, la matemática ha evolucionado basándose en el cálculo y las mediciones, junto con el estudio sistemático de la forma y el movimiento de los objetos físicos. Las matemáticas, desde sus comienzos, han tenido un fin práctico.
Las explicaciones que se apoyaban en la lógica aparecieron por primera vez con la matemática helénica, especialmente con los Elementos de Euclides. La matemática siguió desarrollándose, con continuas interrupciones, hasta que en el Renacimiento las innovaciones matemáticas interactuaron con los nuevos descubrimientos científicos. Como consecuencia, hubo una aceleración en la investigación que continúa hasta la actualidad.
Hoy día, la matemática se usa en todo el mundo como una herramienta esencial en muchos campos, incluso disciplinas que, aparentemente, no están vinculadas con ella, como la música.
Las matemáticas aplicadas, rama de la matemática destinada a la aplicación del conocimiento matemático a otros ámbitos, inspiran y hacen uso de los nuevos descubrimientos matemáticos y, en ocasiones, conducen al desarrollo de nuevas disciplinas.
Los matemáticos también participan en la matemática pura, sin tener en cuenta la aplicación, aunque las aplicaciones prácticas de la matemática pura suelen ser descubiertas con el paso del tiempo.
Sociedad[editar · editar código]
Para acercar las matemáticas a la sociedad, concretamente a los no matemáticos, la comunidad matemática ha aunado esfuerzos en torno a la divulgación de las matemáticas.
En prácticamente todos los lugares del mundo existen competiciones de matemáticas que permiten a los jóvenes aprender y disfrutar con las matemáticas. Especialmente cabe destacar la organización de las diferentes fases de la Olimpiada Matemática, que culmina con la celebración de la Olimpiada Matemática Internacional. Son varios los países participantes en la Olimpiada Matemática Internacional.
Cada 4 años, la Unión Matemática Internacional organiza el Congreso Internacional de Matemáticos.
Matemáticos[editar · editar código]
Un especialista en la matemática es un matemático.
Referencias[editar · editar código]
- ↑ «The unreasonable effectiveness of mathematics in the natural sciences». Richard Courant lecture in mathematical sciences. 11 de mayo de 1959. Communications in Pure and Applied Mathematics. "The miracle of the appropriateness of the language of mathematics for the formulation of the laws of physics is a wonderful gift which we neither understand nor deserve."