Grafo

Grafo etiquetado con 6 vértices y 7 aristas.

Un grafo es una estructura de matemáticas formada por una pareja del conjunto de vértices y del multiconjunto de aristas que da a cada par de vértices una arista o no.

Típicamente, un grafo se representa gráficamente como un conjunto de puntos (vértices o nodos) unidos por líneas (aristas o arcos).

Desde un punto de vista práctico, los grafos permiten estudiar las interrelaciones entre unidades que interactúan unas con otras. Por ejemplo, una red de computadoras puede representarse y estudiarse mediante un grafo, en el cual los vértices representan terminales y las aristas representan conexiones (las cuales, a su vez, pueden ser cables o conexiones inalámbricas).

Prácticamente cualquier problema puede representarse mediante un grafo, y su estudio trasciende a las diversas áreas de las ciencias exactas y las ciencias sociales.

Por lo general, un grafo se representa en forma de diagrama como un conjunto de puntos o círculos para los vértices, unidos por líneas o curvas para los bordes. Los grafos son uno de los objetos de estudio de las matemáticas discretas.

Los grafos son el tema básico estudiado por la teoría de grafos. La palabra grafo fue utilizada por primera vez en este sentido por James Joseph Sylvester en 1878 debido a una relación directa entre las matemáticas y la estructura química (lo que él llamó una imagen químico-gráfica).

Historia

Los siete puentes de Königsberg

El primer artículo científico relativo a grafos fue escrito por el matemático suizo Leonhard Euler en 1736.

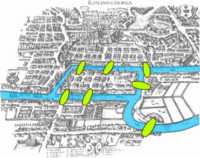
Euler se basó en su artículo en el Problema de los puentes de Königsberg. La ciudad de Kaliningrado (originalmente Königsberg) es famosa por sus siete puentes que unen ambas márgenes del río Pregel con dos de sus islas. Dos de los puentes unen la isla mayor con la margen oriental y otros dos con la margen occidental. La isla menor está conectada a cada margen por un puente y el séptimo puente une ambas islas. El problema planteaba si es posible dar un paseo comenzando desde cualquiera de estas regiones, pasando por todos los puentes, recorriendo solo una vez cada uno y regresando al mismo punto de partida.

Planteándolo con la teoría de grafos, Euler consigue demostrar que el grafo asociado al esquema de puentes de Königsberg no tiene solución, es decir, no es posible regresar al vértice de partida sin pasar por alguna arista dos veces. De hecho, Euler resuelve el problema más general para determinar que condiciones debe satisfacer un grafo para garantizar que se puede regresar al vértice de partida sin pasar por la misma arista más de una vez? Si definimos como <<grado>> al número de líneas que se encuentran en un punto de un grafo, entonces la respuesta al problema es que los puentes de un pueblo se pueden atravesar exactamente una vez si, salvo a lo sumo dos, todos los puntos tienen un grado par.

Definiciones

Grado de un vértice: número de aristas a las que es incidente, informalmente, número de aristas que recibe contando con los bucles a ella misma.

Grafo simple: si ninguna arista es bucle ni múltiple.

Grafo completo: si es simple y todo par de vértices tiene una arista.

Grafo conexo: Si cada par de vértices está conectado por un camino. Si un grafo es conexo, si existe un vértice tal que el grafo sin el vértice es conexo. Un grafo es conexo si y sólo si admite un árbol generador.

Grado ciclo: grafo conexo regular de grado 2 (un camino simple cerrado).

Grafo árbol: grafo conexo sin ciclos. En un árbol, el número de vértices es igual al número de aristas mas uno. Es grafo árbol si para cualesquiera dos vértices existe un único camino de p a q.

Grafo bipartito: grafo tal que su conjunto de vértices puede particionarse en dos conjuntos independientes, en cada conjunto los vértices no se unen y cada vértice del primer conjunto puede o no unirse con un vértice del segundo conjunto. Un grafo es bipartito si y sólo si no contiene ningún ciclo de orden impar.

Grafo planear: si se puede dibujar en el plano de forma que las aristas no se corten (sólo se encuentran en los vértices).

La suma de los grados de los vértices de un grafo es igual a dos veces el número de aristas.

Teorema de Veblen

Un grafo tiene una descomposición en ciclos si y sólo si todo vértice tiene grado par.

Isomorfismo de grafos

Dados grafos con vértices y aristas (V, E) y (V′, E′), una biyección ϕ:V → V′ es isomorfismo si la multiplicidad de la arista p a q en E coincide con la multiplicidad de ϕ(p) a ϕ(q) en E′ para todo p, q ∈ V.

Si dos grafos son isomorfos, entonces son iguales.

Si un grafo es isomorfo a otro, los complementarios también han de serlo.

Propiedades

Grado conexo es euleriano si y sólo si el grado de todo vértice es par. Admite camino euleriano abierto si y sólo si el grado es impar por exactamente 2 vértices.

Matriz de adyacencia

La matriz de adyacencia es una matriz simétrica que representa un grafo. Por ejemplo, del grafo:

• 

La matriz de adyacencia sería:

${\begin{bmatrix}2&1&0&0&1&0\\1&0&1&0&1&0\\0&1&0&1&0&0\\0&0&1&0&1&1\\1&1&0&1&0&0\\0&0&0&1&0&0\end{bmatrix}}$